numpy.random.power

numpy.random.power(a, size=None)

Draws samples in [0, 1] from a power distribution with positive exponent a - 1.

Also known as the power function distribution.

Parameters:

a : float or array_like of floats

Parameter of the distribution. Should be greater than zero.

size : int or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. If size is None (default), a single value is returned if a is a scalar. Otherwise, np.array(a).size samples are drawn.

Returns:

out : ndarray or scalar

Drawn samples from the parameterized power distribution.

Raises:

ValueError

If a < 1.

Notes

The probability density function is

P(x; a) = ax^{a-1}, 0 \le x \le 1, a>0.

The power function distribution is just the inverse of the Pareto distribution. It may also be seen as a special case of the Beta distribution.

It is used, for example, in modeling the over-reporting of insurance claims.

References

[R257]

Christian Kleiber, Samuel Kotz, “Statistical size distributions in economics and actuarial sciences”, Wiley, 2003.

[R258]

Heckert, N. A. and Filliben, James J. “NIST Handbook 148: Dataplot Reference Manual, Volume 2: Let Subcommands and Library Functions”, National Institute of Standards and Technology Handbook Series, June 2003. http://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/powpdf.pdf

Examples

Draw samples from the distribution:

>>> a = 5. # shape
>>> samples = 1000
>>> s = np.random.power(a, samples)

Display the histogram of the samples, along with the probability density function:

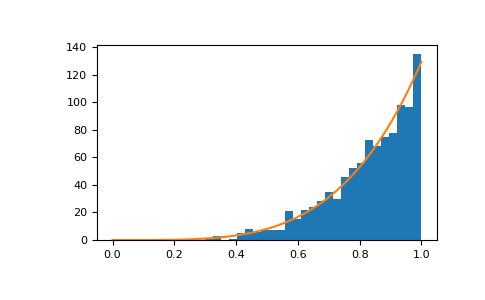
>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, bins=30)
>>> x = np.linspace(0, 1, 100)
>>> y = a*x**(a-1.)
>>> normed_y = samples*np.diff(bins)[0]*y
>>> plt.plot(x, normed_y)
>>> plt.show()

(Source code, png, pdf)

Compare the power function distribution to the inverse of the Pareto.

>>> from scipy import stats
>>> rvs = np.random.power(5, 1000000)
>>> rvsp = np.random.pareto(5, 1000000)
>>> xx = np.linspace(0,1,100)
>>> powpdf = stats.powerlaw.pdf(xx,5)

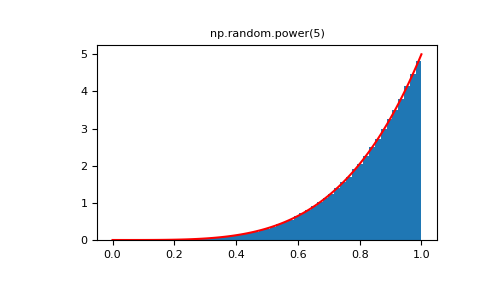
>>> plt.figure()
>>> plt.hist(rvs, bins=50, normed=True)
>>> plt.plot(xx,powpdf,'r-')
>>> plt.title('np.random.power(5)')

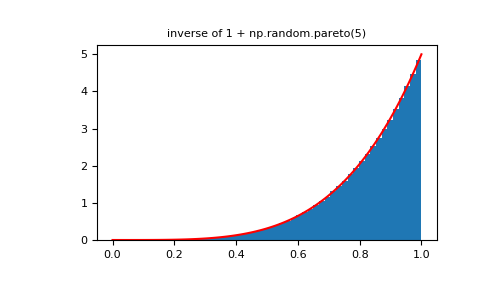
>>> plt.figure()
>>> plt.hist(1./(1.+rvsp), bins=50, normed=True)
>>> plt.plot(xx,powpdf,'r-')
>>> plt.title('inverse of 1 + np.random.pareto(5)')

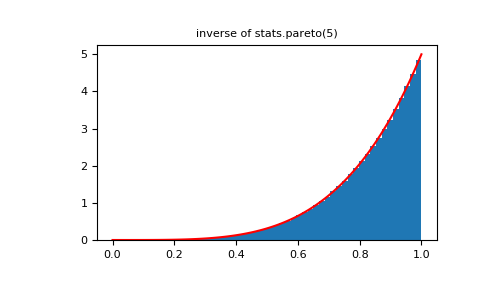
>>> plt.figure()
>>> plt.hist(1./(1.+rvsp), bins=50, normed=True)
>>> plt.plot(xx,powpdf,'r-')
>>> plt.title('inverse of stats.pareto(5)')

(png, pdf)

(png, pdf)

(png, pdf)